Etude des profils
Présentation théorique de l’étude des profils d’ailes par l’approximation des profils minces ainsi que la méthode et les calculs de résolution du problème directement depuis une feuille Excel.
Les équations régissant la physique des fluides forment un système ouvert. Les variables d’états et inconnues du système sont, sauf dans les cas simples, plus nombreuses que les équations à notre disposition (les 5 équations Navier-Stocks).
Il n’y a donc pas de solution analytique dans la formulation générale des problèmes de mécanique des fluides. (Si vous trouvez la solution vous êtes le prochain pour le Nobel de physique ou le prix Abel.)
Il est donc nécessaire d’utiliser des modèles simplifiés pour approcher la réalité.
Hypothèses des profils minces.
Nature de l’écoulement :
- incompressible
- permanent (pas de variation au cours du temps)
- irrotationnel (pas de point mort dans l’écoulement donc pas de turbulence)
- parfait (condition de glissement aux parois)
- sans force de masse (on néglige les effets gravitationnels)
- sans apport de chaleur (on néglige les effets thermodynamiques)
Géométrie de l’aile :
- allongement A=∞ (on néglige les effets de bord)
- épaisseur relative (épaisseur max / corde) <10%
- cambrure relative (flèche max /corde ) <5%
Décomposition de la vitesse :
On définit une vitesse perturbée δV de telle sorte que la vitesse V en un point de l’écoulement soit la somme de la vitesse en infini amont V∞ et de la vitesse perturbée.
Conditions de glissement :
Le fluide étant parfait, les parois de l’obstacle sont des lignes de courant. La vitesse est donc tangente aux parois. En connaissant l’évolution des parois on peut ainsi en déduire l’évolution de la vitesse au parois puis dans le reste du fluide.
Décomposition du profil :
- l’écoulement du profil peut être vu comme la somme de deux écoulements :
- l’écoulement du profil squelettique (ou profil mince) en incidence composé de la corde moyenne du profil réel.
- l’écoulement du profil épais (ou profil symétrique) en répartissant également l’épaisseur autour de la corde moyenne.
- décomposer ainsi le profil permet de séparer l’étude de la portance et l’étude de l’écoulement.
Simplifications mathématiques
Connaissant les lois générales de la physique des fluides (équations de conservation de masse, de mouvement et d’énergie) il serait possible de résoudre directement les équations (mais ca risque d’être assez dur). C’est pourquoi, en plus des simplifications sur la nature physique du problème, on effectue des simplifications mathématiques aux fonctions pour se ramener à des cas simples dont nous connaissons les résultats.
1 : Approximation polynomiale
On approche la fonction (ici la fonction qui définit l’intrados ou l’extrados du profil par un polynôme d’ordre 6 qui est le maximum possible avec Excel) de type :
2 : Série de Fourier
l’approximation par série de Fourier est une autre méthode qui approxime la fonction avec une somme de cosinus et de sinus de la forme :
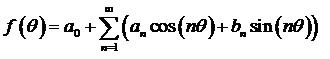
3 : Transformation de Joukowski
La transformation de Joukowski permet de transposer le problème sur le plan complexe
l’obstacle se transforme en cylindre ce qui simplifie la résolution du calcul de l’écoulement.
Caractéristiques du profil
coefficient de pression
coefficient de portance
coefficient de trainée
moment de tangage
foyer aérodynamique
incidence de portance nulle
braquage du volet
Résultats littéraux
Après calcul, transformation et simplification on obtient deux formules :
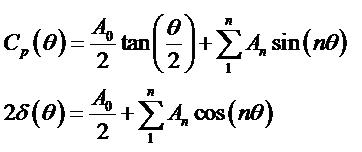La formule de la pente locale du profils δ et la répartition de pression Cp autour du profil.
Il suffit maintenant d’identifier les coefficients An pour connaitre le reste. Pour ce faire il faut partir soit de la formule du profil que l’on a dessiné pour obtenir la répartition de pression et donc les forces aérodynamiques agissant sur le profil. C’est le problème direct.
A l’inverse il est tout a fait possible de partir sur des contraintes de force et de chercher le squelette du profil qui permettrai de générer les forces voulues. C’est le problème indirect.
A incidence nulle :
- coefficient de portance :
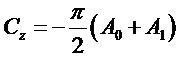
- coefficient de trainée de forme :
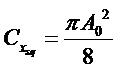
- coefficient du moment de tangage en un point de coordonnée Xa :
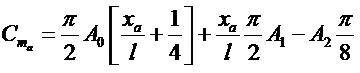
- coefficient du moment de tangage au foyer aérodynamique :
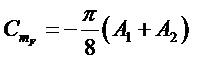
- incidence de portance nulle :
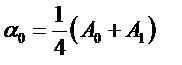
mise en incidence :
la variation d’incidence (delta alpha) modifie les coefficients An
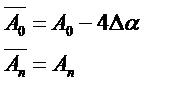on a donc un nouveau coefficient de portance :
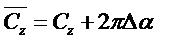
- effet de la gouverne.
il est possible de calculer les variations apportées par le braquage de la gouverne.
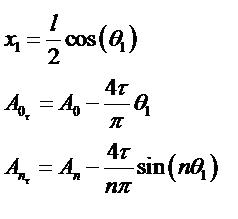
Méthode de résolution du problème direct
1 : tracer le profil a étudier sur du papier millimétré
2 : entrer les coordonnées du profil réel sur Excel
3 : sur le graphique du profil réel relever les coefficients des courbes d’intrados et d’extrados approchées
- où trouver les coefficients ?
4 : entrer les coefficients sur la feuille de calcul
5 : Excel calcule la pente locale du profil approché en dérivant les polynômes d’approximation.
6 : On obtient les courbes et les polynômes approchés du profil squelettique et épais
7 : entrer les coordonnées de la vitesse amont ainsi que l’angle d’attaque.
,
date de publication : 28 mars 2011,
date de dernière mise à jour : 15 décembre 2009
Soutenez l'association en partageant cette page autour de vous :
|